Os processos para fatorar polinômios são denominados: fatoração por agrupamento, fatoração completa, fatoração da diferença de dois quadrados, fatoração pelo fator comum em evidência, fatoração do trinômio quadrado perfeito, fatoração do trinômio do segundo grau, fatoração da soma ou diferença de dois cubos, fatoração por artifício.
[editar]Fatoração pelo fator comum em evidência
Considere o polinômio 14ab + 7bc, seu fator comum em evidência é 7b, dividindo cada termo do polinômio pelo fator comum em evidência 14ab:7b = 2a e 7bc:7b = c, a forma fatorada de um polinômio pelo fator comum em evidência é igual ao produto do fator comum em evidência pelo polinômio obtido da divisão de cada termo do polinômio, logo a forma fatorada de 14ab + 7bc = 7b.(2a +c). O fator comum em evidência pode ser aplicado em todos os termos do polinômio.
Outros exemplos:
15x + 9y = 3.(5x + 3y)
50 − 10y = 10.(5 − y)
[editar]Fatoração por agrupamento
Observe o polinômio ab − b2 + 2a − 2b. Este polinômio não possui um fator comum para ser aplicado em todo o mesmo, a solução é fazer pequenos grupos de polinômios a partir do polinômio principal, veja:
ab − b2 + 2a − 2b = (ab − b2) + (2a − 2b), logo podemos fatorar os pequenos grupos formados do polinômio principal:
ab − b2 = b(a − b)
2a − 2b = 2(a − b), obtemos a fatoração de ab − b2 + 2a − 2b = b(a − b) + 2(a − b), nota-se que os termos entre parênteses são iguais, permitindo uma nova aplicação do fator comum em evidência: (a − b)(b + 2). A forma fatorada de ab − b2 + 2a − 2b = b(a −b) + 2(a − b) = (a − b)(b + 2).
Outro exemplo:
a4 − a5 + a2b − a3b = a2(a2 − a3) + b(a2 − a3) = (a2 − a3)(a2 + b)
[editar]Fatoração da diferença de dois quadrados
Considere o polinômio
m2 − n2, que é uma diferença de dois quadrados, para fatorar o mesmo devemos obter a raiz quadrada do primeiro termo

menos a raiz quadrada do segundo termo
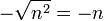
, logo temos
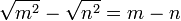
, devemos, agora, multiplicar o polinômio resultante das raizes dos termos iniciais pelo seu oposto:
(m− n).(m + n), logo a fatoração da diferença de dois quadrados é igual à raiz quadrada do primeiro termo menos a raiz quadrada do segundo termo vezes o oposto:

, ou simplesmente
m2 − n2 = (m − n).(m + n).
Outros exemplos:
(n + 8)2 − 1 = [(n + 8) + 1].[(n + 8) − 1] = [n + 8 + 1].[n + 8 − 1] = [n + 9].[n + 7]
a4 − b4 = (a2 + b2).(a2 − b2) = (a − b).(a + b).(a2 + b2)
[editar]Fatoração do trinômio quadrado perfeito
Considere o polinômio 4x2 + 4xy + y2, que é um trinômio quadrado perfeito, pois representa (2x + y)2, mas como saber se um trinômio é ou não quadrado perfeito?
Ainda considerando o polinômio
4x2 + 4xy + y2, vamos obter a raiz quadrada do primeiro termo

e a raiz quadrada do terceiro termo

, finalmente multiplicamos por dois o produto das raízes para verificar se o resultado é igual ao segundo termo do polinômio (
4xy):
2.2x.y = 4xy, o resultado é igual ao segundo termo do polinômio, logo o mesmo é um trinômio quadrado perfeito e sua forma fatorada é
4x2 + 4xy + y2 = (2x + y)2.
Outro exemplo:

ou
x2 − 8xy + 16y2 = (x − 4y)2[editar]Fatoração da soma ou da diferença de dois cubos
Observe a multiplicação resolvida através da propriedade distributiva:
(a + b).(a2 − ab + b2) = a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3, tendo este cálculo como base, podemos dizer que
a3 + b3 = (a + b).(a2 − ab + b2), logo, a fatoração do polinômio
a3 + b3 é igual à raiz cúbica do primeiro termo
![\sqrt[3]{a^3}=a](http://upload.wikimedia.org/math/7/3/5/7354f78ed458baa469352115adbeaf74.png)
, mais a raiz cúbica do segundo termo
![\sqrt[3]{b^3}=b](http://upload.wikimedia.org/math/6/8/1/68126baf717dea11691aefedaf2ef668.png)
vezes o quadrado do primeiro termo
a2, o produto dos dois termos com o sinal oposto
− ab mais o quadrado do segundo termo
b2, formando:
a3 + b3 = (a + b).(a2 − ab + b2).
Outros exemplos:
x3 − y3 = (x − y).(x2 + xy + y2)
[editar]Fatoração do trinômio do segundo grau
Observe o trinômio x2 − 2x − 35, cuja forma fatorada é (x − 7).(x + 5), para realizar sua fatoração devemos obter dois números que somados dêem o coeficiente do segundo termo do polinômio (-2x) e multiplicados dêem o terceiro termo do polinômio (-35), e escrevê-los como produto de dois termos entre parênteses, veja outros exemplos:
a2 + 8a + 12 = (a + 2).(a + 6)
x2 − 15x − 100 = (x − 20).(x + 5)
y2 + y − 72 = (y + 9)(y − 8)
[editar]Fatoração completa
A fatoração completa implica na união de todos os métodos de fatoração de polinômios para tornar um polinômio fatorado ao máximo, ou seja, que não pode ser mais fatorado. Considere o polinômio x4 − y4, que é a diferença de dois quadrados, fatorando-o temos: x4− y4 = (x2 − y2).(x2 + y2), note que o primeiro termo da fatoração [(x2 − y2)] é uma diferença de dois quadrados, devemos fatora-lo:x4 − y4 = (x2 − y2).(x2 + y2) = (x − y).(x + y).(x2 + y2), assim, temos a fatoração completa do polinômio x4 − y4.
Outros exemplos:
3x2 − 6x + 3 = 3.(x2 − 2x + 1) = 3.(x − 1)2
a2 + 2ab + b2 − c2 = (a + b)2 − c2 = (a + b − c)(a + b + c)
[editar]Fatoração por artifício
Em alguns casos, a fatoração só é possível com a utilização de algum artifício. Exemplo;
Fatore a expressão algébrica: x4 + 4x2y2 + 16y4.
(x4 + 4x2y2 + 16y4 + 4x2y2) − 4x2y2 =
x4 + 8x2y2 + 16y4 − 4x2y2 = (x2 + 4y2)2 − 4x2y2 = (x2 + 4y2 + 2xy)(x2 + 4y2 − 2xy)
Artifício utilizado: Adicionamos e subtraímos o termo 4x2y2, não alterando, assim, o valor da expressão e possibilitando a obtenção de trinômio quadrado perfeito para a realização da expressão.
Outro exemplo:
Artifício utilizado: soma-se e subtrai-se

, obtendo-se logo em seguida uma soma de cubos:
[editar]Polinômios irredutíveis
Alguns polinômios não podem ser fatorados, estes são chamados de
polinômios irredutíveis. Por exemplo, o polinômio

é irredutível, pelo
critério de Eisenstein, com
p = 2. Note-se, porém, que a irreducibilidade está sempre condicionada ao corpo considerado; pelo
teorema fundamental da álgebra, todo polinômio tem uma raiz, portanto este polinômio pode ser escrito como

, sendo

uma raiz.
FONTE: WIKIPÉDIA
 menos a raiz quadrada do segundo termo
menos a raiz quadrada do segundo termo 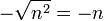 , logo temos
, logo temos 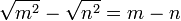 , devemos, agora, multiplicar o polinômio resultante das raizes dos termos iniciais pelo seu oposto: (m− n).(m + n), logo a fatoração da diferença de dois quadrados é igual à raiz quadrada do primeiro termo menos a raiz quadrada do segundo termo vezes o oposto:
, devemos, agora, multiplicar o polinômio resultante das raizes dos termos iniciais pelo seu oposto: (m− n).(m + n), logo a fatoração da diferença de dois quadrados é igual à raiz quadrada do primeiro termo menos a raiz quadrada do segundo termo vezes o oposto:  , ou simplesmente m2 − n2 = (m − n).(m + n).
, ou simplesmente m2 − n2 = (m − n).(m + n). e a raiz quadrada do terceiro termo
e a raiz quadrada do terceiro termo  , finalmente multiplicamos por dois o produto das raízes para verificar se o resultado é igual ao segundo termo do polinômio (4xy): 2.2x.y = 4xy, o resultado é igual ao segundo termo do polinômio, logo o mesmo é um trinômio quadrado perfeito e sua forma fatorada é 4x2 + 4xy + y2 = (2x + y)2.
, finalmente multiplicamos por dois o produto das raízes para verificar se o resultado é igual ao segundo termo do polinômio (4xy): 2.2x.y = 4xy, o resultado é igual ao segundo termo do polinômio, logo o mesmo é um trinômio quadrado perfeito e sua forma fatorada é 4x2 + 4xy + y2 = (2x + y)2. ou x2 − 8xy + 16y2 = (x − 4y)2
ou x2 − 8xy + 16y2 = (x − 4y)2![\sqrt[3]{a^3}=a](http://upload.wikimedia.org/math/7/3/5/7354f78ed458baa469352115adbeaf74.png) , mais a raiz cúbica do segundo termo
, mais a raiz cúbica do segundo termo ![\sqrt[3]{b^3}=b](http://upload.wikimedia.org/math/6/8/1/68126baf717dea11691aefedaf2ef668.png) vezes o quadrado do primeiro termo a2, o produto dos dois termos com o sinal oposto − ab mais o quadrado do segundo termo b2, formando:a3 + b3 = (a + b).(a2 − ab + b2).
vezes o quadrado do primeiro termo a2, o produto dos dois termos com o sinal oposto − ab mais o quadrado do segundo termo b2, formando:a3 + b3 = (a + b).(a2 − ab + b2).
![\frac{x^6}{64}-\frac{y^6}{729}=\left (\frac{x^3}{8}-\frac{y^3}{27} \right ).\left (\frac{x^3}{8}+\frac{y^3}{27} \right )=\left [\left (\frac{x}{2}-\frac{y}{3} \right ).\left (\frac{x^2}{4}+\frac{xy}{6}+\frac{y^2}{9} \right ) \right ].\left [\left (\frac{x}{2}+\frac{y}{3} \right ).\left (\frac{x^2}{4}-\frac{xy}{6}+\frac{y^2}{9} \right ) \right ]](http://upload.wikimedia.org/math/0/0/a/00a50e788393a705bbe1cd23f78bed4c.png)

 , obtendo-se logo em seguida uma soma de cubos:
, obtendo-se logo em seguida uma soma de cubos:
 é irredutível, pelo critério de Eisenstein, com p = 2. Note-se, porém, que a irreducibilidade está sempre condicionada ao corpo considerado; pelo teorema fundamental da álgebra, todo polinômio tem uma raiz, portanto este polinômio pode ser escrito como
é irredutível, pelo critério de Eisenstein, com p = 2. Note-se, porém, que a irreducibilidade está sempre condicionada ao corpo considerado; pelo teorema fundamental da álgebra, todo polinômio tem uma raiz, portanto este polinômio pode ser escrito como  , sendo
, sendo  uma raiz.
uma raiz.


 A neve é uma forma de precipitação. Tudo começa quando o ar quente do solo, mais leve, encontra um ar mais frio acima e pode condensar o vapor d’água contido na forma de gotículas ou cristais de gelo, formando as nuvens.
A neve é uma forma de precipitação. Tudo começa quando o ar quente do solo, mais leve, encontra um ar mais frio acima e pode condensar o vapor d’água contido na forma de gotículas ou cristais de gelo, formando as nuvens.
0 comentários:
Postar um comentário