No cálculo algébrico, algumas expressões representadas por produtos de expressões algébricas, aparecem com muita frequência. Pela importância que representam no cálculo algébrico, essas expressões são denominadas Produtos Notáveis[1]
Quadrado da soma de dois termos
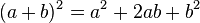
.
Regra básica: Quadrado do primeiro, mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo.


[editar]Quadrado da diferença de dois termos
A expressão diferença do quadrado da soma apenas pelo sinal da segunda parcela:
Regra básica: Quadrado do primeiro termo, menos duas vezes o primeiro vezes o segundo , mais o quadrado do segundo

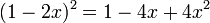
[editar]Produto da soma pela diferença de dois termos
Regra básica: Quadrado do primeiro termo menos o quadrado do segundo termo

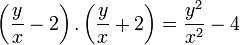
[editar]Cubo da diferença de dois termos

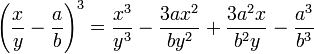

[editar]Cubo da soma de dois termos

Decomposição volumétrica do binômio ao cubo
O cubo da soma de dois termos se diferencia do cubo da diferença apenas pelos sinais


[editar]Quadrado da soma de três termos



[editar]Produto de Stevin (produto de 2 binômios com um termo comum)
Considerando o produto notável

, temos:



[editar]Produto de Warring
Considerando

, temos:
(a + b).(a2 − ab + b2) = a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3 / ,
Considerando
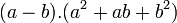
, temos:
Fonte: Wikipedia.
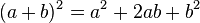 .
.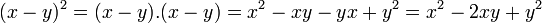
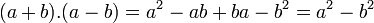


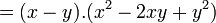

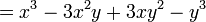

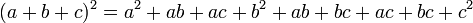

 , temos:
, temos:

 , temos:
, temos:

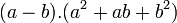 , temos:
, temos: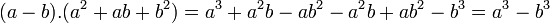

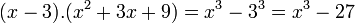



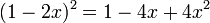

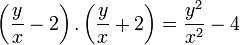

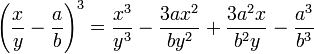













 A neve é uma forma de precipitação. Tudo começa quando o ar quente do solo, mais leve, encontra um ar mais frio acima e pode condensar o vapor d’água contido na forma de gotículas ou cristais de gelo, formando as nuvens.
A neve é uma forma de precipitação. Tudo começa quando o ar quente do solo, mais leve, encontra um ar mais frio acima e pode condensar o vapor d’água contido na forma de gotículas ou cristais de gelo, formando as nuvens.
0 comentários:
Postar um comentário